Números Reales

¿Cómo está conformado el conjunto de los reales?

Para determinar cómo está conformado el conjunto de los números Reales (R) haremos primero una revisión acerca de los distintos conjuntos numéricos.

El conjunto de los números Naturales (N) está formado por los números enteros positivos, es decir, “…son los números que se utilizan para contar.” (Zapico, I.; Micelli, M.; Tajeyan, S. y Vera Ocampo, J., 2006, p. 11).

Debido a su función de contar es que, históricamente, fueron los primeros en aparecer:

1, 2, 3, 4…

Si a estos números se les agregan los números enteros negativos y el cero se obtiene el conjunto de los números Enteros (Z):

…-3, -2, -1, 0, 1, 2, 3….

Sin embargo, los números Enteros no son suficientes si se necesita representar cantidades que no sean enteras, como por ejemplo: 2,5.

Existe otro conjunto que incluye, además de los números antes mencionados,  también a los números que no son enteros; siempre que éstos puedan expresarse como fracción. Es el conjunto de los números Racionales (Q).

Cabe destacar que todo número entero puede expresarse como cociente de dos números enteros, por lo que los Enteros están incluidos en el conjunto de los Racionales.

Pueden citarse los siguientes ejemplos de números racionales:

En síntesis, puede definirse a los números Racionales como aquellos números que pueden expresarse mediante una fracción. Pero no todos los números cumplen esta condición, existen números que poseen infinitas cifras decimales no periódicas y, por lo tanto, no pueden representarse mediante una fracción. Estos se denominan irracionales.

Como por ejemplo:

Todas las raíces no exactas de base entera son números irracionales.

Hay números irracionales que son más conocidos  que otros por su importancia basada en sus múltiples aplicaciones, es el caso de los números: p, j y e.

Los irracionales por sí solos no constituyen un conjunto numérico como los Naturales, Enteros y Racionales, sino que son un subconjunto de los Reales (R).

“El conjunto de los números Reales (R) está formado por los números Racionales (Q) y los irracionales.” (Berio, A.; Colombo, M.; D’Albano, C.; Sardella, O. y Zapico, I., 2001, p. 10).

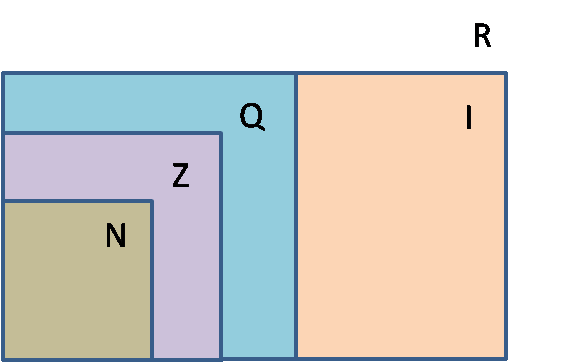
        De esta manera pueden establecerse las siguientes relaciones entre los conjuntos numéricos: “…los Naturales están incluidos en los Enteros, éstos en los Racionales y el conjunto de los Racionales está incluido en el de los Reales.” (Zapico, I.; Micelli, M.; Tajeyan, S. y Vera Ocampo, J., 2006, p. 32).